Biography
My research focuses on developing probabilistic machine learning methods and Bayesian inference techniques to study the thermodynamics and atomic structure of liquid-state materials. I work at the intersection of molecular simulation, statistical mechanics, and data-driven modeling, with an emphasis on uncertainty quantification and interpretable predictions. A core aspect of my work involves using Gaussian Process models and Bayesian approaches to improve the accuracy and reliability of molecular dynamics simulations, particularly in modeling many-body interactions and complex fluid behavior. More broadly, my research aims to integrate physics-based simulation with machine learning to develop flexible, data-efficient models for predicting the structure and thermodynamics of condensed-phase systems.
This website features an overview of my research projects, publications, and presentations, along with teaching resources and course materials. I also share occasional posts and Jupyter notebooks that highlight practical machine learning techniques, statistical mechanics derivations, and computational methods relevant to modeling atomic interactions and thermodynamic behavior. The goal of this site is to provide both an accessible summary of my work and a technical resource for researchers interested in probabilistic modeling and molecular simulation.
- Neutron Scattering
- Molecular Dynamics
- Statistical Mechanics
- Quantum Mechanics
- Probabilistic Machine Learning
- Gaussian Processes
Ph.D. in Chemical Engineering, 2024
University of Utah
B.E. in Chemical Engineering and Mathematics, 2019
Ohio State University
Projects
Bayesian Force Field Optimization
Structure and self-assembly are complex, emergent properties of matter that are often poorly captured by conventional molecular simulation models. Both statistical mechanics and empirical studies have shown that incorporating structural experimental data—such as scattering measurements—can significantly improve the accuracy, transferability, and physical consistency of classical force fields.
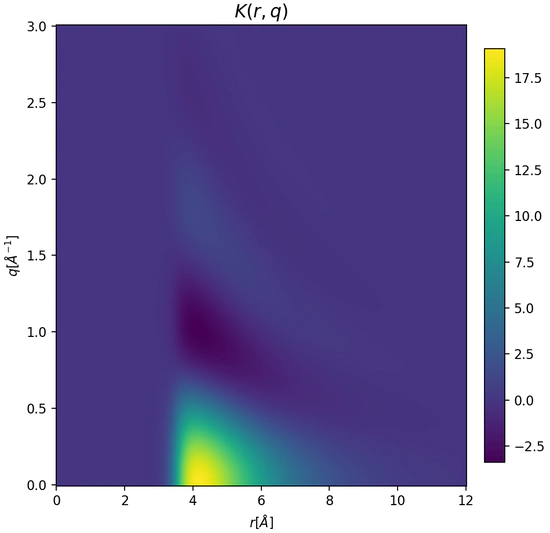
Gaussian Processes for Molecular Simulation
Gaussian processes can model complex experimental data and interatomic interactions while enabling rigorous uncertainty quantification and propagation within a Bayesian framework. We apply state-of-the-art GP methods, including spectral and non-stationary kernel designs [1], to develop next-generation molecular simulation tools such as uncertainty-aware machine learning potentials .
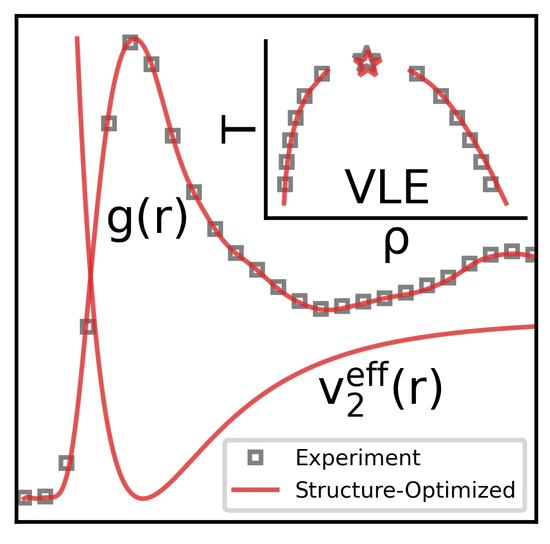
Structure Optimized Potential Refinement (SOPR)
Structure-optimized potential refinement (SOPR) is a machine learning assisted iterative Boltzmann inversion method designed to predict accurate and transferable interaction potentials from a provided set of site-site partial radial distribution functions.