Biography
My research focuses on developing probabilistic machine learning methods and Bayesian inference techniques to study the thermodynamics and atomic structure of liquid-state materials. I work at the intersection of molecular simulation, statistical mechanics, and data-driven modeling, with an emphasis on uncertainty quantification and interpretable predictions. A core aspect of my work involves using Gaussian Process models and Bayesian approaches to improve the accuracy and reliability of molecular dynamics simulations, particularly in modeling many-body interactions and complex fluid behavior. More broadly, my research aims to integrate physics-based simulation with machine learning to develop flexible, data-efficient models for predicting the structure and thermodynamics of condensed-phase systems.
This website features an overview of my research projects and publications, along with teaching resources and course materials. I will also share occasional posts and Jupyter notebooks that highlight practical machine learning techniques, statistical mechanics derivations, and computational methods relevant to modeling atomic interactions and thermodynamic behavior. The goal of this site is to provide both an accessible summary of my work and a technical resource for researchers interested in probabilistic modeling and molecular simulation.
- Bayesian Inference
- Probabilistic Machine Learning
- Gaussian Processes
- Neutron and X-ray Scattering
- Molecular Dynamics
- Statistical Mechanics
- Quantum Mechanics
Ph.D. in Chemical Engineering, 2024
University of Utah
B.E. in Chemical Engineering and Mathematics, 2019
Ohio State University
Projects
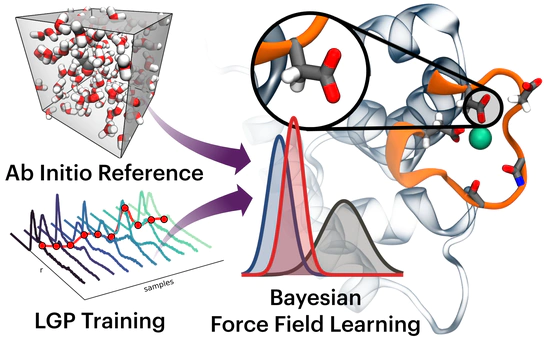
Force Field Design with Bayesian Learning
Bayesic Force Fields (BFF) is an open source, Bayesian force field learning tool aimed at addressing transferability and robustness issues with existing biomolecular force fields. The code performs efficient Bayesian inference with physically motivated priors on Coulombic, bonded, and non-bonded terms.
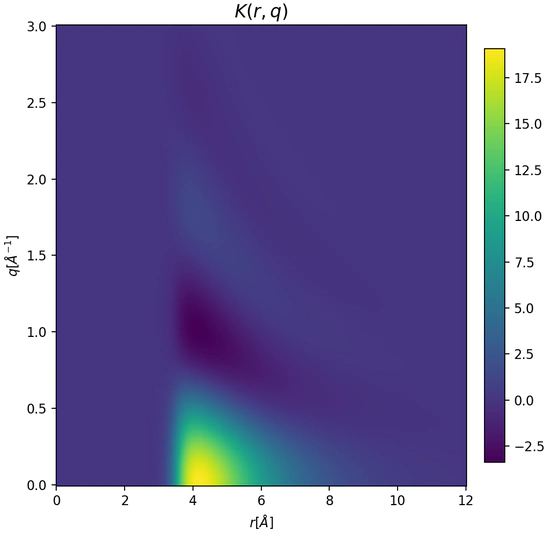
Gaussian Processes for Molecular Modeling
Gaussian processes can model complex experimental data and interatomic interactions while enabling rigorous uncertainty quantification and propagation within a Bayesian framework. We apply state-of-the-art GP methods, including local [1], spectral, and non-stationary kernel design [2], to develop next-generation molecular simulation tools.
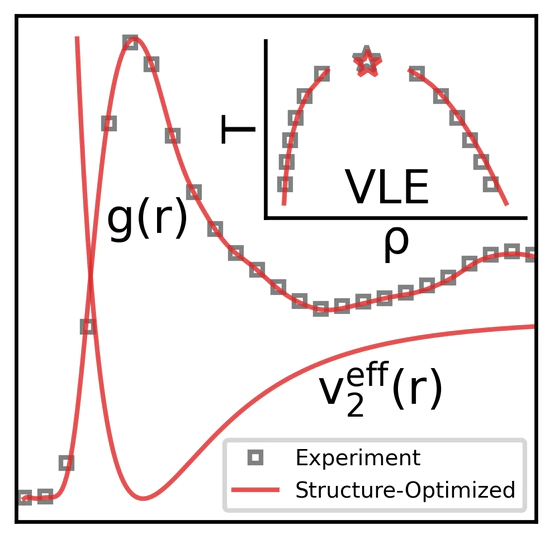
Gaussian Process Interatomic Potentials
Gaussian processes (GPs) are a Bayesian regression technique with big upside for machine learning interatomic potentials. Unlike black-box methods like neural networks, GPs are interpretable, uncertainty-aware, and allow for the integration of physics-informed behavior through the use of carefully designed Bayesian priors.